Você também desenvolve plugins para o AutoCAD e não é um programador experiente?
Hoje vou falar um pouco sobre a importância de aprender sobre algoritmos e desempenho.
Se você é um programador experiente, já deve ter ouvido falar da análise de complexidade de um algoritmo.
Se não é, em linhas gerais significa comparar dois ou mais algoritmos com a mesma finalidade e saber dizer qual é mais eficiente. Não vou me ater demais na teoria, então sugiro ver este documento.
Vamos ver um exemplo prático.
Na análise de colisão de objetos no BIM, esse processo pode ser bem demorado se você não escreveu um algoritmo eficiente. NO SOLIDOS isso é feito pelo comando SINTERF, que verifica se dois dispositivos colidem. Quando isso acontece, você tem de alterar a geometria da rede (afundar a rede, reposicionar o poço de visita).
Se tivéssemos 100 dispositivos, quantas colisões teríamos de testar?
Um programador inexperiente talvez dissesse: "Temos de testar todos contra todos". Isso significa 100 x 100, ou 10.000 interações (aproximadamente, veja o documento!!!). Na análise de complexidade diríamos que este é um algoritmo de complexidade O(n^2), o proporcional ao quadrado do número de itens a testar
Um programador um pouco mais esperto diria: "Se testei A contra B, não preciso testar B contra A", então, teríamos cerca de n*(n-1)/2 iterações, o que já é bem menos que a primeira opção. Neste caso, 4950.
Mas veja, no caso especifico do SOLIDOS, estamos num loteamento, ou cidade. Qual o tamanho médio de um dispositivo? Um PV, talvez 1,50 x 1,50 m. Um tubo, talvez tenha em média uns 50 a 100 metros. Isso significa que testar a colisão de um PV com outro a mais de 3m de distância é completamente supérfluo, percebe? E o tubo? Bem, esse complica um pouco, pois ele costuma ser muito comprido em relação a largura, então temos de levar isso em conta.
Na API de programação do AutoCAD, para verificar se 2 sólidos colidem, podemos fazer:
interfere = solidoA.CheckInterference(solidoB)
Só que essa operação da API, é um tanto lenta, ainda mais para sólidos "complexos"
Se esse teste custasse 200 milissegundos em média e tivéssemos 100 dispositivos:
- testar todos contra todos, ignorando que solidoA.CheckInterference(solidoB) é igual a solidoB.CheckInterference(solidoA) (complexidade = n^2): 10.000 testes ou 2000s = 33 minutos.
- testando sem repetir (complexidade = n*(n-1)/2), 4950 iterações, ou 16 minutos, menos ruim, mas ainda péssimo.
Vamos melhorar isso.
Primeiro, não precisa usar o método CheckInterference sempre. Podemos testar o GeometryExtents do sólido. O GeometryExtents é o menor paralelepípedo alinhado com os sistema de coordenadas WCS (World Coordinate System) do AutoCAD, que contem o sólido. Com ele podemos fazer:
Function VerificarInterferencia(solidoA As Solid3d, solidoB As Solid3d) As Boolean
Dim geo1 As Extents3d = solidoA.GeometricExtents
Dim geo2 As Extents3d = solidoB.GeometricExtents
If geo2.MinPoint.X > geo1.MaxPoint.X OrElse
geo2.MaxPoint.X < geo1.MinPoint.X OrElse
geo2.MinPoint.Y > geo1.MaxPoint.Y OrElse
geo2.MaxPoint.Y < geo1.MinPoint.Y OrElse
geo2.MinPoint.Z > geo1.MaxPoint.Z OrElse
geo2.MaxPoint.Z < geo1.MinPoint.Z Then Return False
Return solidoA.CheckInterference(solidoB)
End Function
Neste código, só testamos a colisão de sólidos se os paralelepípedos (GeometricExtents) colidem. Note que o teste no paralelepípedo é matemático, o que demora MUITO menos
Lembra que eu falei que testar dois sólidos muito distantes é supérfluo? E se classificássemos a nossa lista de dispositivos de tal forma que agrupamos aqueles mais próximos entre si, e testamos a colisão nesses agrupamentos ?
Primeiro, como classificar esses dispositivos em grupos de proximidade?
Bom, temos o "GeometryExtents" , podemos usar ele.
Primeiro imagine uma malha, com células cuja largura é condizente com o tamanho médio dos dispositivos, por exemplo: 50 a 100 metros. Veja um algoritimo que calcula a largura máxima dessas células e agrupa esses sólidos:
Dim dicExtents As New Dictionary(Of Dispositivo, Extents3d)
Dim dicMalha As New Dictionary(Of String, List(Of Dispositivo))
Dim larg As Double = 0
'calcula a maior largura
For Each disp As Dispositivo In Dispositivos
Dim dispExtents = disp.GeometricExtents
larg = Math.Max(larg, dispExtents.MaxPoint.X - dispExtents.MinPoint.X)
larg = Math.Max(larg, dispExtents.MaxPoint.Y - dispExtents.MinPoint.Y)
dic(disp) = dispExtents
Next
larg = Math.Ceiling(larg)
'classifica em função dessa largura
For Each kv In dicExtents
Dim dispExtents = kv.Value
Dim xMin = Math.Floor(dispExtents.MinPoint.X / larg) * larg
Dim xMax = Math.Floor(dispExtents.MaxPoint.X / larg) * larg
Dim yMin = Math.Floor(dispExtents.MinPoint.Y / larg) * larg
Dim yMax = Math.Floor(dispExtents.MaxPoint.Y / larg) * larg
For x = xMin To xMax Step larg
For y = yMin To yMax Step larg
Dim hash = CInt(x) & "," & CInt(y)
Dim lista As List(Of SolDevice)
If dicMalha.ContainsKey(hash) Then
lista = dicMalha(hash)
Else
lista = New List(Of SolDevice)
dicMalha(hash) = lista
End If
lista.Add(kv.Key)
Next
Next
Next
O primeiro looping, percorre a lista de dispositivos, armazenando no dicionário "dicExtents" o paralelepípedo que circunscreve o dispositivo e calcula a maior largura entre eles.
O segundo looping, agrupa o sólido nas células que ele "pode" ter colisões. Note que usei um tipo de função "hash" que permite que mais de um dispositivo tenha o mesmo "hash". O que é um hash?
A hash (Resumo) é qualquer algoritmo que mapeie dados grandes e de tamanho variável para pequenos dados de tamanho fixo. Por esse motivo, as funções Hash são conhecidas por resumirem o dado (veja esta matéria).
Quando faço:
Dim xMin = Math.Floor(dispExtents.MinPoint.X / larg) * larg
Estou pegando o X do canto inferior esquerdo do paralelepípedo e "simplificando ele para o "X" do vértice inferior esquerdo da célula mais próxima. Repetindo o processo para "Y", faço uma "hash" que é a coordenada do vértice inferior esquerdo da célula. Acompanhou até aí?
Fazendo o mesmo com o canto superior direito e iterando entre as células deste intervalo, tenho as células onde possivelmente o sólido vai colidir. Note, poderia incluir o Z, em vez de uma malha bidimensional, teria uma tridimensional.
Com a "hash", coloco o dispositivo na lista (o agrupamento) daquela célula.
Note, que se calculássemos a complexidade deste algoritimo, teríamos algo como:
- Complexidade linear para calcular o "GeometryExtents" (ou seja, diretamente proporcional ao número de dispositivos)
- Complexidade linear para classificar na os sólidos
Agora, Para cada célula da malha que efetivamente tem sólidos, calculamos as colisões fazendo o teste "todos contra todos" mais "esperto", que sabem que:
solidoA.CheckInterference(solidoB) é igual a solidoB.CheckInterference(solidoA)
Note:
No pior dos piores casos, teremos apenas uma célula e cairemos na complexidade n * (n-1) / 2 iterações
É seguro dizer que, no nosso exemplo (colisão de dispositivos numa cidade ou loteamento), teremos mais de 1 célula e mesmo que tenhamos dispositivos em todas as células, cada uma delas terá um número reduzido de dispositivos. Então teremos um somatório de iterações que realmente demoram (CheckInterference), muito reduzido:
Número de iterações pesadas = (número de células) * (número médio de dispositivos) * ( (número médio de dispositivos) - 1 ) / 2
Na pasta suporte do SOLIDOS, tem um DWG, com 107 dispositivos. Ao rodarmos o comando que verifica as colisões (SINTERF), teremos as seguintes células (em vermelho) com largura de cerca de 130 metros (o maior tubo):
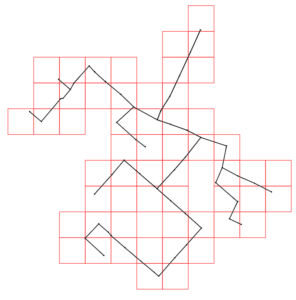
Esta malha tem 56 células, a que tem mais dispositivos tem 10 dispositivos. Em média temos 3 em cada célula, então teremos aproximadamente 321 (calculando 56*3*(3-1)/2) iterações pesadas (aquelas que demoram), o que é bem próximo do numero real, 311 neste DWG. Se cada uma demorar 200 milissegundos, teremos algo em torno de 1 minuto, ou 33 VEZES menos que o algoritmo do programador totalmente iniciante e 16 VEZES menos que o algoritimo do programador "intermediário".
Preciso dizer que a escala de tempo do AutoCAD algo como "4 segundos da vida real" igual a "4 HORAS no AutoCAD" (hehehe)?
Se você chegou até aqui, dá uma conferida no meu livro!!!
