Culverts Design - Channel

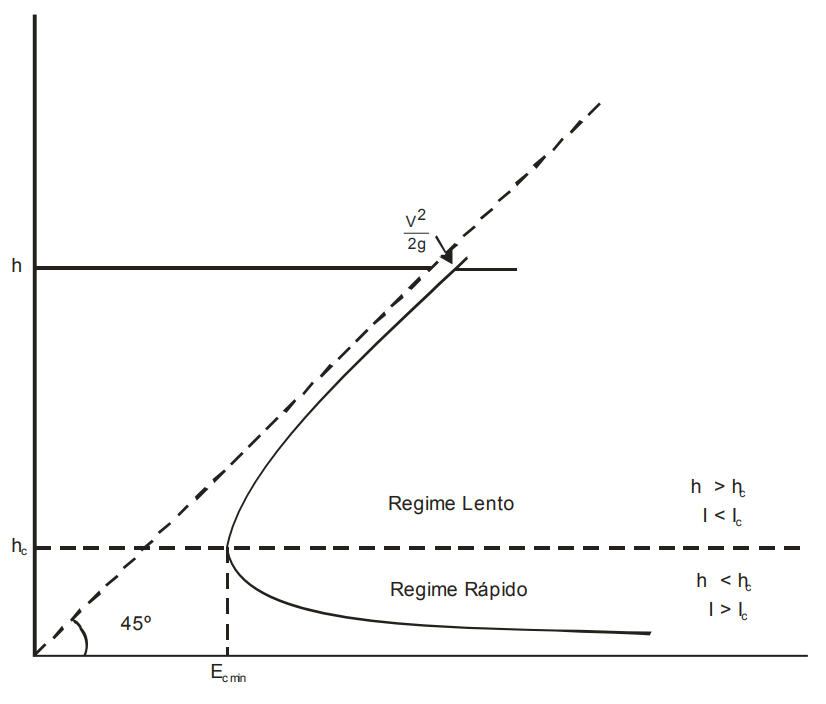
1. Critical flow operation
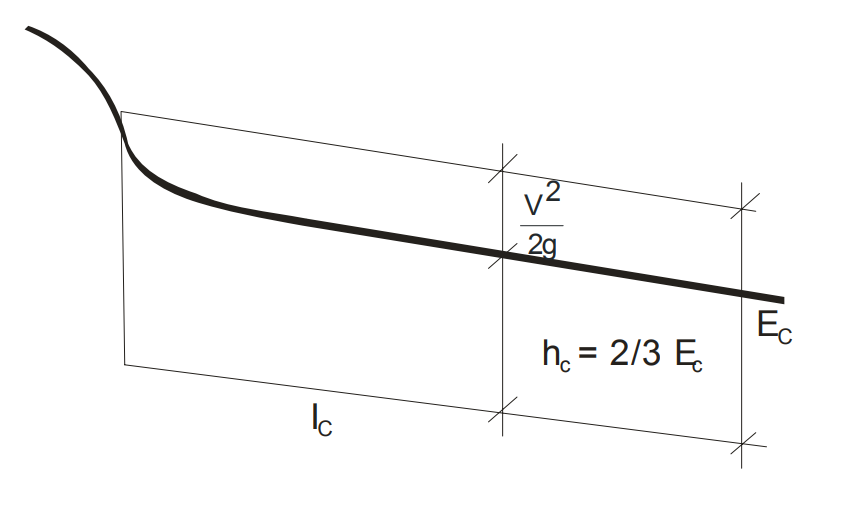
   • Ec = D
   • hc = (2/3) * Ec
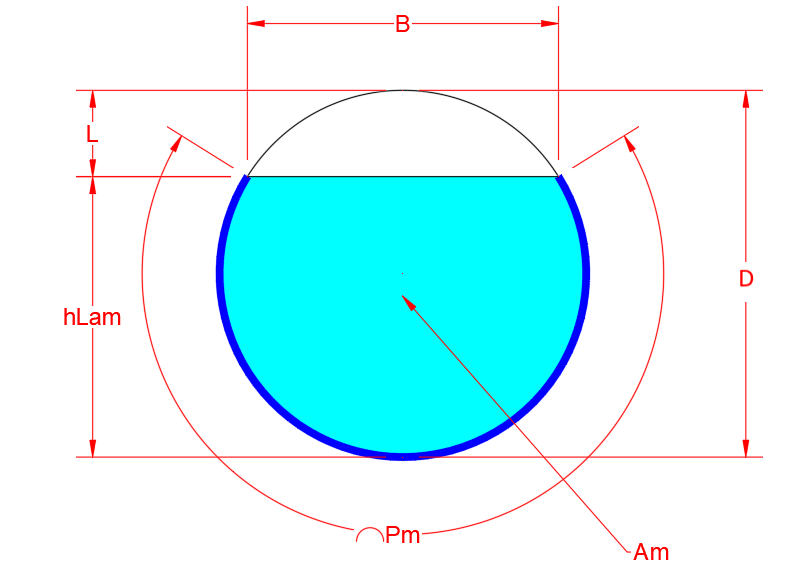
   • Am = function(section, hLam), the image refers to a circular section, but it can be any type of section (rectangular, circular, elliptical, etc.). For double, triple culverts, etc., Am and Pm add up to all sections
   • Pm = function(section, hLam)
   • B = function(section, hLam)
   • Rh = Am / Pm
   • hLam ≤ D; arbitrate hLam that satisfies Fr = 1 (critical flow condition)
   • Qcalc = g ^ 0.5 * Am * (Am / B) ^ 0.5
   • Vcalc = Qcalc / Am
   • Icalc = n ^ 2 * Vcalc ^ 2 / (Rh ^ (4 / 3))
   • Vc = (g * hc) ^ 0.5
   • Fr = Vcalc / Vc
   • For Fr = 1 (condition of critical flow ):
     • Qc = Qcalc
     • Vc = Vcalc
     • Ic = Icalc
     • dc = hc = hLam
   • Note: Vc is the critical velocity for Fr=1. In the dimensioning of sewage networks, NBR 9649, item 5.1.5.1, the so-called critical velocity is given by:
     Vcr = 6 * (g * Rh) ^ 0.5
     This is the critical velocity that occurs in the pipe, for the current slope situation of the project, which has no obligation to be equal to the critical slope where Fr=1. Being thus, the Froude number given by Fr = Vesc / (g * yh) ^ 0.5, can be different from 1.
   Where:
   • n - Manning's coefficient
   • D - Culvert section height
   • hLam - arbitrary flow height
   • Am - wet section area as a function of flow height (hLam) in the adopted section (circular, rectangular, etc
   • B - width of the free board, which is in contact with the atmosphere
   • Qcalc - calculated flow for an arbitrary flow height (hLam)
   • Vcalc - calculated speed for arbitrary flow height (hLam)
   • Icalc - calculated slope of the culvert that causes Vcalc and Qcalc in the section and (hLam) arbitrated
   • Ec - specific energy
   • hc - critical depth
   • Fr - Froude number
   • dc - critical tie
   • Qc - flow in the critical flow condition (Fr = 1)
   • Vc - flow velocity in the critical flow condition (Fr = 1)
   • Ic - culvert slope for critical flow condition (Fr = 1)
2. Culvert operation in the supercritical flow
   Limiting its permissible capacity to the flow corresponding to the critical flow, with energy specific equal to its diameter or height, which requires upstream protection and downstream of erosion risks.
   For this condition:
   • Qesc ≤ Qadm
   • V ≤ Vadm
   • Qadm = Qc
   • HW ≤ D (inlet not submerged)
   • TW ≤ dc
   Where:
   • Qesc - project discharge, the flow to be drained
   • Qadm - allowable flow in section
   • Vadm - permissible speed, according to DNIT, 4.5 m/s for concrete pipes; If V > Vadm, you can:
     • decrease the slope of the culvert
     • change the section
   • HW - upstream (inlet) flow height
   • TW - downstream (outlet) flow height
3. Culvert operation in the subcritical flow
   Whenever the slope of the culvert (I) is less than the critical (Ic), the dimensioning (section and flow velocity) will be obtained through the general flow equations.
   In this condition:
   • I < Ic
   • Limitations:
     • cellular, lenticular, elliptical: hLam ≤ 0.80 * D
     • lenticular, elliptical: hLam ≥ 0.20 * D
     • lenticular: dc ≤ 0.65 * D
     • elliptical: dc ≤ 0.72 * D
   • Am = function(section, hLam)
   • Pm = function(section, hLam)
   • Rh = Am / Pm
   • Vcalc = Rh ^ (2 / 3) * I ^ 0.5 / n
   • Qcalc = Am * V
   Where:
   • Ic - critical slope, slope for which the culvert operates under the critical flow (Ec=D, Fr=1)
   • hLam - arbitrary flow height
   • I - culvert design slope
   • Am - wet section area for hLam height
   • Pm - wet section perimeter for height hLam
   • Rh - hydraulic radius
   • dc - critical tie (see critical flow)
   • Vcalc - flow velocity calculated by the Manning formula, for a flow height hLam
   • Qcalc - flow flowing into the culvert for the arbitrated hLam height
   • Qesc - design flow, the flow that should flow into the culvert
   Arbitrate hLam until Qcalc = Qesc