Triangulação de Delaunay
O algoritmo implementado em todos os softwares que produzem triangulação, ele chama-se “Triangulação de Delaunay”.
Da Wikipédia:
Em matemática, uma Triangulação de Delaunay para um conjunto de pontos P no plano é uma triangulação DT(P)
onde nenhum ponto em P está dentro da circunferência formada por qualquer triângulo na DT(P).
A Triangulação de Delaunay maximiza o menor ângulo de todos os triângulos na triangulação;
esta tende a evitar triângulos com ângulos internos muito pequenos.
De forma simplificada o algoritmo é:
- Tome três pontos quaisquer
- Desenhe um círculo que passe por estes três pontos
- Verifique se existe um quarto ponto dentre deste círculo
- Se não existir, este é um triângulo válido se ele não sobrepõe outros triângulos
- Se existir, este triângulo é inválido
- Repita a todos os pontos até esgotar os pontos sem sobrepor
Note que cada ponto no algoritmo tem apenas coordenadas X e Y. NÃO É CONSIDERADA a coordenada Z. Assim, assim todos os triângulos estão com Z=0.
Somente após a triangulação é que o “Z” é aplicado aos vértices da triangulação.
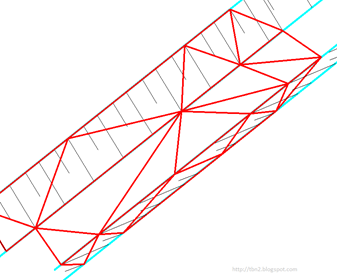
Se observarmos a triangulação gerada sem proceder qualquer alteração, é fácil perceber que alguns triângulos não traduzem uma superfície do terreno correta, por exemplo, num talude, esperamos que os mesmos estejam sobre o talude, ligando o pé com a crista. Mas pode ser que a crista da margem direita triangule com a crista da margem esquerda:
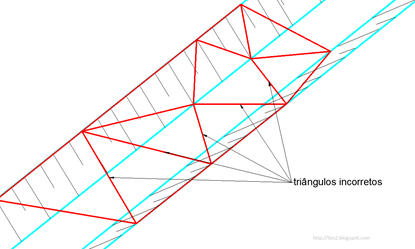
A figura abaixo mostra o MDT, já tratado com linhas obrigatórias: