Stepping Stone Method

The stepping-stone method reaches the optimal solution starting from an initial solution and is researching a better solution can be obtained. As part of the method an initial solution must find a feasible solution to be able to use any method.

There are several methods that can be used to obtain a feasible initial solution: all of them, however, are based on the maximum amount that may be allocated to any cell of the transport matrix.

done the allocation, eliminates the row (or column) of matrix in which it reached the supply (demand), and proceeds to choosing to allocate another cell, until no there are more remains of supply and demand.

However methods differ regarding the choice Cell. There are three methods that are commonly presented in the literature:

• Northwest Corner Method
  this method, the cell allocation is chosen for that lies more to the north as possible and still have supply and demand
• Low Cost Method
  this method, the selected cell is the smallest unit shipping cost, and we still have supply and demand
• method of Vogel or Penalties
  is to allocate the maximum amount of transport in the cell whose penalty by Your choice is non- maximal. This penalty is associated with each row and column, and is estimated by the difference between the two lower costs of each row and column. The row or column that has the largest fee will be utilized to determine the cell in which the allocation is made.

DDM program implements the Northwest Corner Method.

Optimization
The algorithm for optimization is:

1. Balancing supply and demand
   If the sum of deals is greater than the demands of , create a fictitious demand with the difference taken in module now if the sum of demands is greater than that of deals, create a fictitious supply with the difference taken in module.
2. Create an initial solution
   You can use the Northwest Corner Method:
   1. Start by variable X11
   2. If still available supply, to pass the variable Xi+1,j
   3. If only search available, move to the variable Xi,j+1
   4. Continue until all the basic variables (those with a circle) and all other variables (not basic) be zero.
3. Test Optimization
   1. Assuming a basic solution:
   2. A Basic Allowable Solution is optimal if and only if: Cij - Ui - Vj = 0
      for all (i, j) where Xij variable is not basic
      
      If the solution is optimal, stop execution but, continue to next step
   3. Select Entry VB (VBE)
      • How Cij - Ui - Vj is the rate at which the objective function will evolve as the non- basic variable Xij increases, the VBE should have a coefficient Cij - Ui - Vj negative value to decrease the total cost
      • VBE will be having coefficient Cij - Ui - Vj more negative or is, X13
   4. Select VB Output
      • Larger VBE will cause a chain reaction, defined by us in jail.
      • So, we will have receptor cells and donor cells, shown in Table Transport by signs + and -
      • This case we use the chain marked in red
      • The amount to be transferred from donor cells to the recipient is given the minimum (x11 = 70, x23 = 75), or 70
      • VBE = x11
      
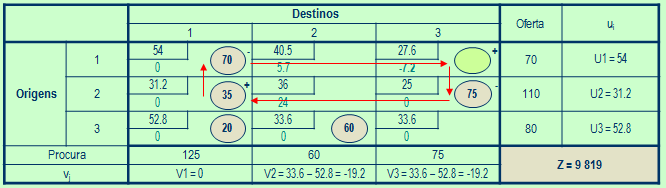
   5. Identify the new basic solution acceptable
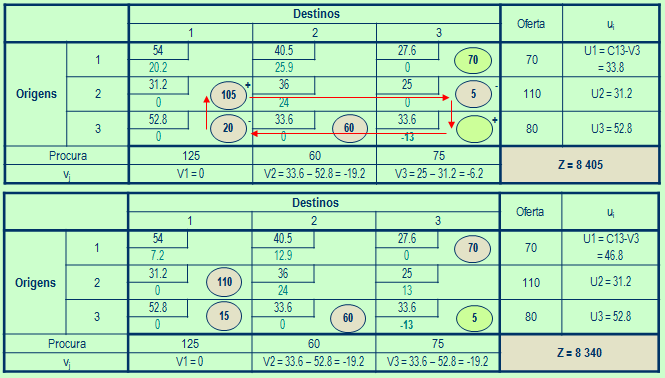
   6. Return to step 1
4. After running the algorithm, all variables are calculated, and the list of basic variables contain the values of VB amounts to ship