Método Stepping Stone

O método de stepping-stone chega à solução ótima partindo se uma solução inicial e pesquisando se alguma solução melhor pode ser obtida.como o método parte de uma solução inicial, devemos encontrar uma solução viável qualquer para poder utilizar o método.

Existem diversos métodos que podem ser utilizados para obter uma solução inicial viável: todos eles, entretanto, fundamentam-se na máxima quantidade que poderá ser alocada em uma célula qualquer da matriz de transportes.

Efetuada a alocação, elimina-se a linha (ou coluna) da matriz na qual se atingiu a oferta (demanda), e procede-se a escolha de uma outra célula para alocar, até que não existam mais sobras de oferta e demanda.

Contudo os métodos se diferenciam em relação a escolha da célula. Existem três métodos que normalmente são apresentados na literatura:

• Método do Canto Noroeste
  neste método, a célula escolhida para alocação é que se situa mais ao noroeste possível e que ainda dispõe de oferta e de demanda
• Método do Custo Mínimo
  neste método, a célula escolhida é a de menor custo unitário de transporte, e que ainda dispõe de oferta e demanda
• Método de Vogel ou das Penalidades
  consiste em atribuir a máxima quantidade de transporte na célula cuja penalidade pela sua não-escolha é máxima. Esta penalidade é associada a cada linha e coluna, e é estimada através da diferença entre os dois menores custos de cada linha e coluna. A linha ou coluna que possuir a maior penalidade será utilizada para determinar a célula na qual a alocação será efetuada.

O programa DDM implementa o Método do Canto Noroeste.

Otimização
O algorítimo para otimização será:

1. Equilibrar ofertas e demandas
   Se a somatória das ofertas for maior que a das demandas, crie uma demanda fictícia com a diferença tomada em módulo, agora, se a somatória das demandas for maior que a das ofertas, crie uma oferta fictícia com a diferença tomada em módulo.
2. Criar uma solução inicial
   Pode-se usar o Método do canto Noroeste:
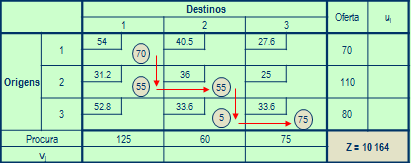
   1. Começar pela variável X11
   2. Se houver ainda oferta disponível, passar para a variável Xi+1, j
   3. Se só houver procura disponível, passar para a variável Xi, j+1
   4. Prosseguir até obter todas as variáveis básicas (as que têm um círculo) e todas as outras variáveis (não básicas) serão zero.
3. Teste de otimização
   1. Assumindo uma solução básica:
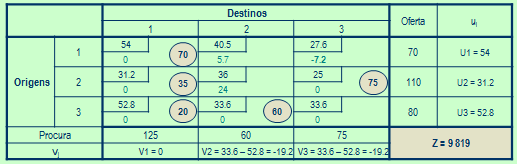
   2. Uma Solução Básica Admissível é ótima se e só se: Cij – Ui – Vj ≥ 0
      para todo (i, j) em que Xij é variável não básica
      
      Se a solução é ótima, pare a execução senão, continue para próximo passo
   3. Escolher a VB Entrada (VBE)
      • Como Cij – Ui – Vj representa a taxa a que a função objetivo irá evoluir à medida que a variável não básica Xij aumenta, a VBE deverá ter um coeficiente Cij – Ui – Vj negativo para diminuir o custo total.
      • A VBE será a que tem coeficiente Cij – Ui – Vj mais negativo, ou seja, X13
   4. Escolher a VB Saída
      • Aumentar a VBE irá provocar uma reação em cadeia, na cadeia por nós definida.
      • Assim, passaremos a ter células receptoras e células fornecedoras, representadas no Quadro dos Transportes pelos sinais + e –
      • Neste caso iremos utilizar a cadeia marcada a vermelho
      • O valor a transferir das células fornecedoras para as receptoras é dado pelo mínimo (x11 = 70, x23 = 75), ou seja, 70
      • VBE = x11
      
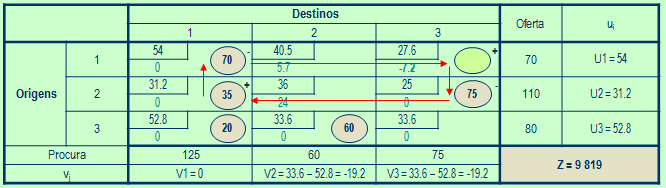
   5. Identificar a nova solução básica admissível
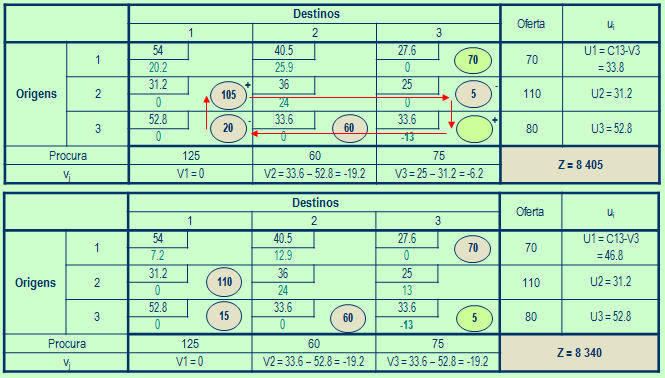
   6. Retorne ao passo 1
4. Após a execução do algorítimo, todas as variáveis estarão calculadas, e a lista de variáveis básicas VB conterá os valores das quantidades a serem transportadas